Basic Proportionality Theorem

Basic Proportionality Theorem:-

For online classes yo can go through mention URL

https://www.youtube.com/watch?v=BXrpbl4jYBc&t=139s

Basic Proportionality Theorem states that "If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio".

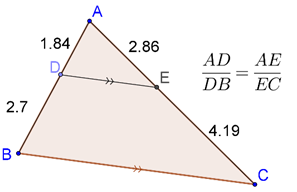
In the following figure, segment $DE$ is parallel to the side $BC$ of $\Delta ABC$. Note how $DE$ divides $AB$ and $AC$ in the same ratio:

---

Proof of Basic Proportionality Theorem:

Given: 

1. $\Delta ABC$
2. $DE\parallel BC$

To prove: $\frac{AD}{DB}=\frac{AE}{EC}$

Construction: 

1. Join $BE$ and $CD$
2. Draw $DP\perp AC$
3. Draw $EQ\perp AB$

Proof: Consider $\Delta AED$. If you have to calculate the area of this triangle, you can take $AD$ to be the base, and $EQ$ to be the altitude, so that:

$$ar\left(\Delta AED\right)=\frac{1}{2}\times AD\times EQ$$

Now, consider $\Delta DEB$. To calculate the area of this triangle, you can take $DB$ to be the base, and $EQ$ (again) to be the altitude (perpendicular from the opposite vertex $E$ ).

Thus,

$$ar\left(\Delta DEB\right)=\frac{1}{2}\times DB\times EQ$$

Next, consider the ratio of these two areas you have calculated:

$$\frac{ar\left(\Delta AED\right)}{ar\left(\Delta DEB\right)}=\frac{\frac{1}{2}\times AD\times EQ}{\frac{1}{2}\times DB\times EQ}=\frac{AD}{DB}$$

In an exactly analogous manner, you can evaluate the ratio of areas of $\Delta AED$ and $\Delta EDC$:

$$\frac{ar\left(\Delta AED\right)}{ar\left(\Delta EDC\right)}=\frac{\frac{1}{2}\times AE\times DP}{\frac{1}{2}\times EC\times DP}=\frac{AE}{EC}$$

Finally, We know that "Two triangles on the same base and between the same parallels are equal in area". Here, $\Delta DEB$ and $\Delta EDC$ are on the same base $DE$ and between the same parallels – $DE\parallel BC$ .

$$\Rightarrow ar\left(\Delta DEB\right)=ar\left(\Delta EDC\right)$$

Considering above results, we can note,

$$\frac{ar\left(\Delta AED\right)}{ar\left(\Delta DEB\right)}=\frac{ar\left(\Delta AED\right)}{ar\left(\Delta EDC\right)}$$

$$\Rightarrow \frac{AD}{DB}=\frac{AE}{EC}$$

This completes our proof of the fact that $DE$ divides $AB$ and $AC$ in the same ratio.

For more Videos.: - https://www.youtube.com/channel/UCnSzn6hUZk-M7juvSAK2Eqw

Odd function & Even Functions

Even Functions

for video classes.: - https://www.youtube.com/watch?v=O178h_HkQss&t=111s

A function is "even" when:

f(x) = f(−x) for all x

This is the curve f(x) = x²+1

They got called "even" functions because the functions x², x⁴, x⁶, x⁸, etc behave like that, but there are other functions that behave like that too, such as cos(x):

Cosine function: f(x) = cos(x)
It is an even function

But an even exponent does not always make an even function, for example (x+1)² is not an even function.

https://www.youtube.com/channel/UCnSzn6hUZk-M7juvSAK2Eqw/videos

Odd Functions

A function is "odd" when:

−f(x) = f(−x) for all x

Note the minus in front of f(x): −f(x).

And we get 

This is the curve f(x) = x³−x

They got called "odd" because the functions x, x³, x⁵, x⁷, etc behave like that, but there are other functions that behave like that, too, such as sin(x):

Sine function: f(x) = sin(x)
It is an odd function

But an odd exponent does not always make an odd function, for example x³+1 is not an odd function.

Neither Odd nor Even

Don't be misled by the names "odd" and "even" ... they are just names ... and a function does not have to be even or odd.

In fact most functions are neither odd nor even. For example, just adding 1 to the curve above gets this:

This is the curve f(x) = x³−x+1

It is not an odd function, and it is not an even function either.
It is neither odd nor even

Even or Odd?

Example: is f(x) = x/(x²−1) Even or Odd or neither?

Let's see what happens when we substitute −x:

f(−x) =(−x)/((−x)²−1)

=−x/(x²−1)

=−f(x)

So f(−x) = −f(x) , which makes it an Odd Function

Even and Odd

The only function that is even and odd is f(x) = 0

Special Properties

Adding:

• The sum of two even functions is even
• The sum of two odd functions is odd
• The sum of an even and odd function is neither even nor odd (unless one function is zero).

For more videos.

https://www.youtube.com/channel/UCnSzn6hUZk-M7juvSAK2Eqw/videos