ABCD Song For Children | Alphabets Song For Children

Basic Proportionality Theorem

Basic Proportionality Theorem:-

For online classes yo can go through mention URL

https://www.youtube.com/watch?v=BXrpbl4jYBc&t=139s

Basic Proportionality Theorem states that "If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio".

In the following figure, segment $DE$ is parallel to the side $BC$ of $\Delta ABC$. Note how $DE$ divides $AB$ and $AC$ in the same ratio:

---

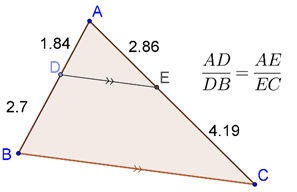
Proof of Basic Proportionality Theorem:

Given: 

1. $\Delta ABC$
2. $DE\parallel BC$

To prove: $\frac{AD}{DB}=\frac{AE}{EC}$

Construction: 

1. Join $BE$ and $CD$
2. Draw $DP\perp AC$
3. Draw $EQ\perp AB$

Proof: Consider $\Delta AED$. If you have to calculate the area of this triangle, you can take $AD$ to be the base, and $EQ$ to be the altitude, so that:

$$ar\left(\Delta AED\right)=\frac{1}{2}\times AD\times EQ$$

Now, consider $\Delta DEB$. To calculate the area of this triangle, you can take $DB$ to be the base, and $EQ$ (again) to be the altitude (perpendicular from the opposite vertex $E$ ).

Thus,

$$ar\left(\Delta DEB\right)=\frac{1}{2}\times DB\times EQ$$

Next, consider the ratio of these two areas you have calculated:

$$\frac{ar\left(\Delta AED\right)}{ar\left(\Delta DEB\right)}=\frac{\frac{1}{2}\times AD\times EQ}{\frac{1}{2}\times DB\times EQ}=\frac{AD}{DB}$$

In an exactly analogous manner, you can evaluate the ratio of areas of $\Delta AED$ and $\Delta EDC$:

$$\frac{ar\left(\Delta AED\right)}{ar\left(\Delta EDC\right)}=\frac{\frac{1}{2}\times AE\times DP}{\frac{1}{2}\times EC\times DP}=\frac{AE}{EC}$$

Finally, We know that "Two triangles on the same base and between the same parallels are equal in area". Here, $\Delta DEB$ and $\Delta EDC$ are on the same base $DE$ and between the same parallels – $DE\parallel BC$ .

$$\Rightarrow ar\left(\Delta DEB\right)=ar\left(\Delta EDC\right)$$

Considering above results, we can note,

$$\frac{ar\left(\Delta AED\right)}{ar\left(\Delta DEB\right)}=\frac{ar\left(\Delta AED\right)}{ar\left(\Delta EDC\right)}$$

$$\Rightarrow \frac{AD}{DB}=\frac{AE}{EC}$$

This completes our proof of the fact that $DE$ divides $AB$ and $AC$ in the same ratio.

For more Videos.: - https://www.youtube.com/channel/UCnSzn6hUZk-M7juvSAK2Eqw