Odd function & Even Functions

Even Functions

for video classes.: - https://www.youtube.com/watch?v=O178h_HkQss&t=111s

A function is "even" when:

f(x) = f(−x) for all x

This is the curve f(x) = x²+1

They got called "even" functions because the functions x², x⁴, x⁶, x⁸, etc behave like that, but there are other functions that behave like that too, such as cos(x):

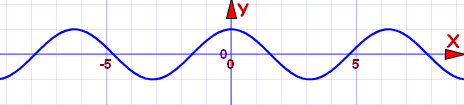
Cosine function: f(x) = cos(x)
It is an even function

But an even exponent does not always make an even function, for example (x+1)² is not an even function.

https://www.youtube.com/channel/UCnSzn6hUZk-M7juvSAK2Eqw/videos

Odd Functions

A function is "odd" when:

−f(x) = f(−x) for all x

Note the minus in front of f(x): −f(x).

And we get 

This is the curve f(x) = x³−x

They got called "odd" because the functions x, x³, x⁵, x⁷, etc behave like that, but there are other functions that behave like that, too, such as sin(x):

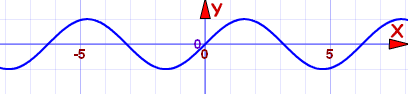
Sine function: f(x) = sin(x)
It is an odd function

But an odd exponent does not always make an odd function, for example x³+1 is not an odd function.

Neither Odd nor Even

Don't be misled by the names "odd" and "even" ... they are just names ... and a function does not have to be even or odd.

In fact most functions are neither odd nor even. For example, just adding 1 to the curve above gets this:

This is the curve f(x) = x³−x+1

It is not an odd function, and it is not an even function either.
It is neither odd nor even

Even or Odd?

Example: is f(x) = x/(x²−1) Even or Odd or neither?

Let's see what happens when we substitute −x:

f(−x) =(−x)/((−x)²−1)

=−x/(x²−1)

=−f(x)

So f(−x) = −f(x) , which makes it an Odd Function

Even and Odd

The only function that is even and odd is f(x) = 0

Special Properties

Adding:

• The sum of two even functions is even
• The sum of two odd functions is odd
• The sum of an even and odd function is neither even nor odd (unless one function is zero).

For more videos.

https://www.youtube.com/channel/UCnSzn6hUZk-M7juvSAK2Eqw/videos